We’ve all seen galleries or videos of zooming into the Mandelbrot set, but not as many for julia sets. This video sums it up, while the boundary of the Mandelbrot set is a map of a number of different julia sets, the julia sets are almost exactly self similar. If you pick 2 areas on a julia set, there is a function that will map one part exactly onto the other. This is true for the linear IFS fractals I’ve been writing apps for.
These maps don’t exist the same way for the Mandelbrot set, which seems strange when the algorithms for generating the images seem so similar. There is a fundamental difference between the two types of objects though. A julia set is defined by one single function and the different points in the image capture the behavior of a starting point. Each point of the Mandelbrot set corresponds to a function, and that to a Julia set. To do the standard rendering each Julia set is reduced to a single numeric value.
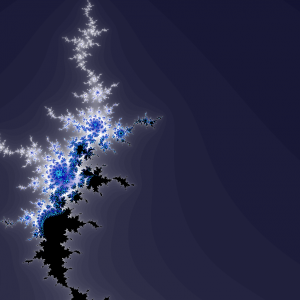
Now, this value hasn’t been chosen at random, but happens to answer a particular question. Is the Julia set of that function connected or is it a dust of disconnected specs? If we don’t care about that question, we can milk the rendering to get some more interesting fractal images. If we move the starting point, then the boundary of our new set moves accordingly. Instead of showing just barely touching Julias, it moves off center and some of the edges stray into the solid territory while others move into the dust realm.
I’ve put together some images using modifications I made to an HTML5 canvas renderer. (Link to my changes here) They show various alternate Mandelbrot sets generated from changing the starting position of the rendering. In further installments we can look at computing other ways to reduce the Julia fractals down to a single value for computing still other Mandelbrots. I’ll also cover generating Mandelbrot sets for the IFS fractals as well. That uses a more complicated algorithm.
These images show what happens when you go off script with the Mandelbrot. There are now pieces floating off the main island and large chunks are cut off at rough but boring boundaries. The transitional areas between the vast boring solid areas and the ethereal dusty areas contain a little burst of activity.
One of the early casualties is the symmetry and regularity of the Mandelbrot set.