Tag: geometric
-
Geometric spiral fractal
Related Images:
-

Generative convergence #1 – Shadows
I wasn’t aiming for something this sparse, or this kind of vertical pattern, but it turned out like a more refined version of some of my other experiments. This method is interpolating a function that resembles a Dirac delta function centered at 1/2, the other lines are reflections of that central spike. Related Images:
-

Technique work
I can’t say I’m a huge fan of these, but I’m playing around with colors and the rendering.  Right now they just seem pretty  for pretty’s sake.  I think I’m waiting around for inspiration on how to put these to good use.  These are generative and then just selected to save as an image.  Enjoy!…
-
Another generative geometric fractal experiment
I’ve got to take a break from the stripey stuff for a little while. This is circling back to the circles. I’ve taken the mapping I’ve been using from the inside of a sphere to the set of all circles, lines and points on the plane and combined them. This is what I was aiming…
-
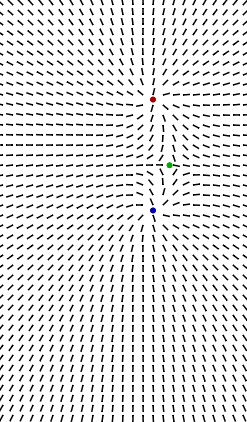
My First canvas experiment
This is my first experiment with canvas. I was trying to build a better understanding of the geometric uses of Clifford algebras. This little snip-it shows some features of the Clifford triple product in 2 dimensional Euclidean space. Related Images:
-

Twist again – more geometric generative op art
After fighting all the overlapping issues with second order equations, I switched back to first order and hard coded a single focus point in the equations. Â With that change I was able to start doing some more predictable plots with the ring functions. Related Images:
-

A single twist and spray
One of the most popular images I’ve developed (I’ve no idea what verb to stick here) is this basic geometric op art style piece. Â I was just using a very simple mask to test out using differential equations to generate families of curves. Â It’s grown on me, and I’m starting to put some more images…