Tag: canvas
-

Nothing fancy: Winter bubbles
My inspiration board on pinterest has been filling up, so I wanted to take a few hours to whip up something quick. I really liked the simplicity of winter trees. I didn’t want to do a direct copy, so this is my riff on the composition. Related Images:
-

Rough and Random page
I’ve had this sitting on my computer for a while and thought I’d publish it rather then just leave it sitting there. This simulates a pulse of light expanding out like my compression wave examples. This time however, we are looking at a pulse of light expanding in the vicinity of a black hole. Rather…
-

Something I’m playing around with.
This is something that I just stumbled onto while working on something else. I’ve taken a quick break from the atomic orbital viewer. I’m trying to make the IFS fractals more visually interesting. One approach is to create Mandelbrot versions of the IFS fractals which should break up the uniformity. Instead of showing one image…
-

I’m thinking about how best to handle this
I like the idea of putting demos up directly on the blog like the last one. However, they don’t show up on feed readers so you either get the text without the image and then click through. I can throw down some javascript to include a place holder link to the demo in the feed,…
-
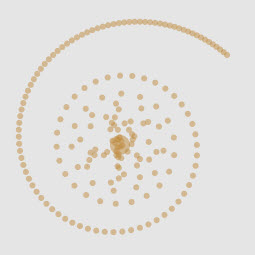
The best surprises come from unexpected places
This time I’m back with some more physics visualizations with a flat 2d canvas. I’m skipping over some demos of basic physics to get at some orbital mechanics animations that I found surprising. I’ve derived and calculated solutions for two objects gravitationally bound to each other from my freshman physics classes back in college. Then…
-

Just a quick update
I’ve uploaded my very very super rough fractal canvas image editor. This is what I’ve been putting the galleries together with. It’s super rough, I’ll be improving it in random fits and spurts, and putting some demo posts up as well. Also, someone please please suggest a decent title for this one. I’ve got nothing.…
-

I’m just playing around with particles for this one
This has come together more quickly than any of the other demos. I wanted to see what I could do with a more abstract particle system driven through the same equations I’ve been using for fractals. The old formulas didn’t have quite enough pizazz, so I moved over to the sylvester library for matrices and…
-

The most basic IFS Fractal of all – the cantor set
What is that, Morse code? That my friends is the cantor set. It is one of the examples of basic topology and one of the objects that highlight many of the non-intuitive aspects of infinities. The most common construction is to take a line and remove the middle third. Next you remove the middle thirds…
-

Speed of sound
I’ve finally written some code that works in IE8.0, chrome and firefox. Rather than drawing complex fractals and solutions to equally archane differential equations, I’m trying to build some simple demos using more easily understood principles and mathematics. Now this is a very simple model that just shows the general principles of how something like…
-
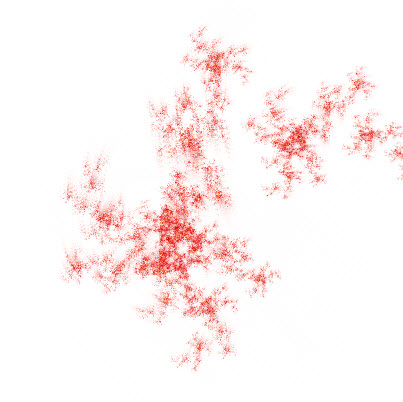
Closer to a good stopping point
I’ve finally got the chrome crashing bug and crazy memory usage fixed, so I’ve taken a little bit of time while my 3 week old daughter is sleeping here and there to add some refinements. I’ve added basic shading back in, added a link to the blog and a couple of bookmarking links. I’m going…